K-Nearest Neighbor Classification(K-최근접 이웃 알고리즘)
- 지도학습 (Supervised Learning)
- K-NN 알고리즘의 원리 : 새로운 데이터의 클래스를 해당 데이터와 가장 가까운 k개 데이터들의 클래스로 결정한다.
- K-NN 알고리즘의 최근접 이웃 간의 거리를 계산할 때 유클리디안 거리, 맨하탄 거리, 민코우스키 거리 등을 사용한다. 대표적으로 유클리디안 거리를 사용한다.
*유클리디안 거리 : 두 점 P와 Q가 각각 P=(p1,p2,p3,...,pn) Q=(q1,q2,q3,...,qn)의 좌표를 가질 때 아래 공식으로 표현된다.

- k의 선택은 학습의 난이도와 데이터의 개수에 따라 결정될 수 있으며, 일반적으로 훈련 데이터 개수의 제곱근으로 설정한다.
- k가 너무 크면 주변 데이터와의 근접성이 떨어질 수 있고, 너무 작으면 이상치 혹은 잡음 데이터와 이웃이 될 가능성이 있으므로 적절한 k개를 선택해야한다.
- KNN 장점
1. 사용이 간단하다.
2. 범주를 나눈 기준을 알지 못해도 데이터를 분류할 수 있다.
3. 추가된 데이터의 처리가 용이하다.
- KNN 단점
1. k값의 결정이 어렵다.
2. 비수치 데이터의 경우 유사도를 정의하기 어렵다.
3. 데이터 내에 이상치가 존재하면 큰 영향을 받는다.
### 파이썬을 이용한 KNN 분석
# 1. 데이터 전처리
# Seaborn 모듈에서 titanic 데이터 로드
import pandas as pd
import seaborn as sns
df = sns.load_dataset('titanic')
# 출력할 열의 개수 15 설정하기
pd.set_option('display.max_columns',15)
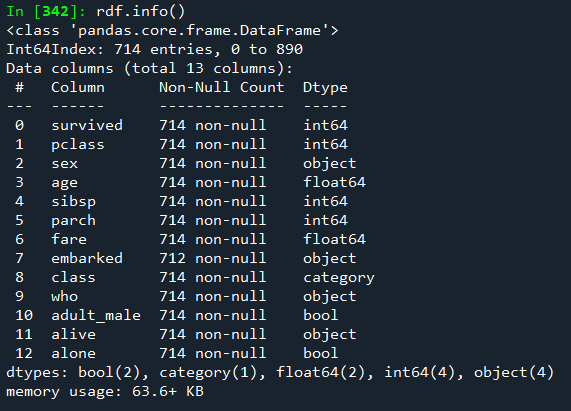
df.info()

# NaN 값이 많은 deck 열을 삭제,
# embarked와 내용이 겹치는 embark_town 열을 삭제
rdf = df.drop(['deck','embark_town'],axis=1)
rdf.info()

# age 열에 나이 데이터가 없는 모든 행을 삭제
rdf = rdf.dropna(subset=['age'],axis=0)
rdf.info()
# embarked 열의 NaN 값을
# 승선도시 중에서 가장 많이 출현한 값으로 치환하기
# 승선도시 중에서 가장 많이 출현한 값
rdf['embarked'].value_counts(dropna=True)
most_freq = rdf['embarked'].value_counts(dropna=True).idxmax()
most_freq
# embarked 열의 NaN 값을 most_freq 값으로 치환하기
rdf['embarked'].fillna(most_freq, inplace=True)
rdf.info()
rdf['embarked'].value_counts()
S 556
C 130
Q 28
# 분석에 활용할 열(속성)을 선택
ndf = rdf[['survived','pclass','sex','age','sibsp','parch','embarked']]
ndf.info()
ndf.describe(include='all')

# get_dummies() : 원핫인코딩 - 범주형 데이터를 모형이 인식할 수 있도록 숫자형으로 변환
onehot_sex = pd.get_dummies(ndf['sex'])
onehot_sex.head()
ndf["sex"].head()
# ndf, onehot_sex 데이터 합하기
ndf = pd.concat([ndf,onehot_sex],axis=1)
ndf.head()
# embarked 데이터를 원핫인코딩으로 변환하기
onehot_embarked = pd.get_dummies(ndf['embarked'],prefix='town')
onehot_embarked.head()
ndf= pd.concat([ndf,onehot_embarked],axis=1)
ndf.head()
# 속성 변수, 설명 변수, 독립 변수
X = ndf[['pclass','age','sibsp','parch','female','male','town_C','town_Q','town_S']]
Y = ndf['survived']
X.head()
# 설명 변수 데이터를 정규화(normalization)
# 분석시 데이터 값의 크기에 따라서 분석의 결과에 영향을 미칠 수 있음
# 나이 범위가 크기 때문에, 정규화를 통해서 모든 속성 변수들의 값을 기준 단위로
# 변경할 필요가 있음
import numpy as np
from sklearn import preprocessing
X = preprocessing.StandardScaler().fit(X).transform(X)
X
# 2. 훈련용 데이터와 검증 데이터 분류
# train data와 test data로 구분 (7:3 비율)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.3, random_state=10)
print('train data 개수:', X_train.shape)
print('test data 개수:', X_test.shape)

# 3. KNN 분류 모형 - sklearn 사용
from sklearn.neighbors import KNeighborsClassifier
# n_neighbors = 5 : k개의 최근접 이웃
# : 최근접 데이터를 n개 선택
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_train, y_train)
y_hat = knn.predict(X_test)
print(y_hat[0:10])
print(y_test.values[0:10])
# 4.모형 성능 평가
from sklearn import metrics
knn_matrix = metrics.confusion_matrix(y_test, y_hat)
print(knn_matrix)
# 5. 모형 성능 평가 - 평가지표 계산
knn_report = metrics.classification_report(y_test,y_hat)
print(knn_report)

# accuracy : 정확도
# macro avg : 단순 평균
# weighted avg : 가중 평균. 표본의 갯수로 가중평균
'''
confusion_matrix
예측값
T [110 15] [TP FP]
F [ 25 65] [TN FN]
T F => 실제 값
TP : True Positive 실제값 T, 예측값 T
FP : False Positive 실제값 F, 예측값T
FN : False Negative 실제값 T, 예측값 F
TN : True Negative 실제값 F, 예측값 F
Precision (정확도)
True로 예측한 대상이 실제 True인 비율
정확도가 높다는 것은 FN 오류 작은 경우를 말한다.
Recall (재현율)
실제값이 True인 분석 대상 중 True로 예측한 비율
재현율이 높다는 것은 FN 오류가 낮다는 것을 말한다.
F1-Score (F1지표)
정확도와 재현율의 조화 평균을 계산한 값
모형의 예측력을 평가 지표
'''
'Python' 카테고리의 다른 글
| Python - 의사결정나무(Decision Tree) (0) | 2021.07.16 |
|---|---|
| Python - SVM(서포트 벡터 머신) (0) | 2021.07.16 |
| Python - 회귀분석(Regression) (0) | 2021.07.15 |
| Python - 서울시 CCTV수를 파악해서 시각화하기 (산점도, 회귀선) (0) | 2021.07.14 |
| Python - 웹크롤링 후 텍스트 마이닝 (seleium) (0) | 2021.07.13 |



