'''
머신러닝 : 기계학습
각각의 변수들의 관계를 찾는 과정. 예측 단계.
예측 : 회귀분석
분류 : KNN
군집 : K-means
...
지도학습 : 회귀분석, 분류
=> 정답을 알고 학습
비지도학습 : 군집
=> 정답이 없는 상태에서 서로 비슷한 데이터끼리 그룹화
강화학습
머신러닝 프로세스
데이터 정리 -> 데이터 분리(훈련데이터/검증데이터) -> 알고리즘 준비
-> 모형학습(훈련데이터) -> 예측(검증데이터) - > 모형평가 -> 모형활용
'''
'''
회귀분석(regression) : 가격, 매출, 주가 등등의 연속성이 있는 데이터의 예측에 사용되는 알고리즘
설명(독립)변수 : 예측에 사용되는 변수
-> 학습 (머신러닝 알고리즘 : 회귀 분석)
-> 예측(종속)변수
'''
# 단순 회귀 분석 : 독립변수 : X / 종속변수 : Y
# Y = aX + b
### 기본 라이브러리 불러오기
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 회귀 분석의 간단한 예
# 공부시간 : 독립변수, 시험점수 : 종속변수
x =[[10],[5],[9],[7]] #공부시간 10,5,9,7시간
y = [100,50,90,77] #시험점수 100,50,90,77점
# y = [[100],[50],[90],[77]] #시험점수 100,50,90,77점
# 시리즈 객체가 아니어도 가능하다.
# 1. 선형회귀분석 객체 생성하기
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
# 2. 선형회귀분석 객체를 이용하여 학습시키기
# 결정계수는 0~1사이의 값으로 높을수록 설명력이 높다고 판단한다.
lr.fit(x,y)
r_square=lr.score(x,y)
r_square

# 3. 예측하기
result = lr.predict([[7],[8]])
print("예상점수",result)

# 간단한 다중회귀분석 예제
from sklearn.linear_model import LinearRegression
x = [[10,3],[5,2],[9,3],[7,3]] #공부시간,학년
y = [[100],[50],[90],[77]] #시험점수
model=LinearRegression()
model = model.fit(x,y)
# 7시간 2학년
result = model.predict([[7,2]])
result

# 6시간 3학년
result = model.predict([[6,3]])
result

df = pd.read_csv('auto-mpg.csv',header=None)
df.columns = ['mpg','cylinders','displacement','horsepower','weight','acceleration','model year','origin','name']
df.head()
print(df.info())
print(df.describe())
print(df.horsepower.unique())
#1. horsepower 컬럼의 ? 값을 결측값으로 변경하기
df['horsepower'].replace('?',np.nan,inplace=True)
df['horsepower'].isnull().sum()
print(df.info())
# dropna() : 누락 데이터 행을 삭제
df.dropna(subset=["horsepower"],axis=0,inplace=True)
print(df.info())
pd.set_option('display.max_columns',10) # 10까지 컬럼 조회하기
print(df.describe()) #horsepower 컬럼이 숫자형이 아니라서 생략된다.
# horsepower 데이터의 형을 문자열을 실수형으로 변환
df['horsepower'] = df['horsepower'].astype('float')
# 분석에 활용할 속성(열)을 선택
# 연비(mpg), 실린더(cylinders), 출력(horsepower), 중량(weight)
ndf = df[['mpg','cylinders','horsepower','weight']]
ndf.info()
# matplot으로 산점도 그리기
# mpg와 weight 두개의 변수를 산점도 작성하기
ndf.plot(kind='scatter',x='weight',y='mpg',c='coral',s=10,figsize=(10,5))
plt.show()
# seaborn으로 산점도 그리기
fig = plt.figure(figsize=(10,5))
ax1 = fig.add_subplot(1,2,1)
ax2 = fig.add_subplot(1,2,2)
sns.regplot(x='weight',y='mpg',data=ndf,ax=ax1)
sns.regplot(x='weight',y='mpg',data=ndf,ax=ax2, fit_reg=False)
plt.show()

# jointplot 그리기
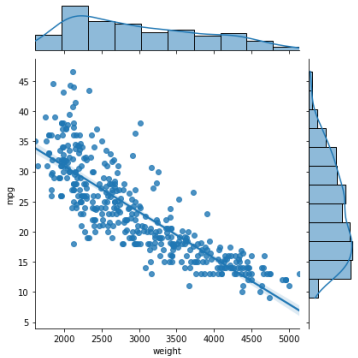
sns.jointplot(x='weight',y='mpg',data=ndf)
sns.jointplot(x='weight',y='mpg',kind='reg',data=ndf)
plt.show()
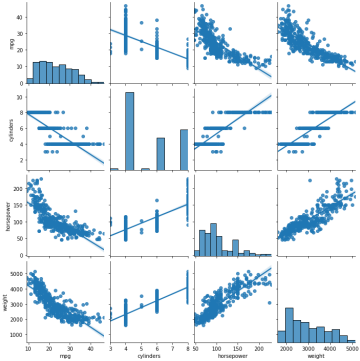
# seaborn pairplot
sns.pairplot(ndf, kind='reg')
plt.show()
# 데이터셋 구분 - 훈련용(train data) / 검증용(test data)
# 독립변수 : X (데이터프레임)
X = ndf[["weight"]]
# 종속변수 : Y (시리즈)
Y = ndf["mpg"]
print(type(Y))
from sklearn.model_selection import train_test_split
# 훈련데이터, 검증데이터 분리(7:3으로 분리)
# random_state=10 : 추출 사용되는 상수. 시드 값과 비슷
# : 분리되는 데이터의 유지성을 위한 설정
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.3, random_state=10)
print('train data 개수:',len(X_train))
print('test data 개수:',len(X_test))
X_train[:10]
# 단순 회귀 분석 모형 - sklearn 사용
# sklearn 라이브러리에서 선형회귀분석 모듈 가져오기
from sklearn.linear_model import LinearRegression
# 단순 회귀 분석 모형 객체 생성
lr = LinearRegression()
# train data를 가지고 모형 학습
# 훈련 데이터. 정답
lr.fit(X_train, y_train) #X_train : 훈련데이터 / y_train :
# 결정계수 (R-제곱)
# 모형의 예측력이 좋은지 판단하는 지표 1에 가까울수록 좋다
r_square = lr.score(X_test, y_test) #결정계수 (R-제곱)
print(r_square)
# 기울기
print("기울기 a", lr.coef_)
# y 절편
print("y 절편 b", lr.intercept_)
# 테스트하기. 전체 데이터를 이용하여 예측하기
# y_hat : 예측한 값
y_hat = lr.predict(X) # 평가
y_hat
# 원래 값 Y와 예측된 값 y_hat 데이터를 그래프로 작성하기
plt.figure(figsize=(10,5))
ax1 = sns.kdeplot(Y, label="Y") #실제 mpg 데이터 그래프
ax2 = sns.kdeplot(y_hat, label='y_hat',ax=ax1)
plt.legend()
plt.show()

'''
산점도 결과를 보면, 직선보다는 곡선의 형태가 더 예측하기 좋다.
단순 선형 회귀 분석은 직선으로 분석하는 방법임
-> 이 데이터에서는 높은 정확도를 위해서는 곡선 형태의 회귀선이 좋다.
다항 회귀 분석 -> 회귀선을 곡선의 형태로 분석 방식
단순회귀분석 : 두 변수간의 관계를 직선 형태로 분석하는 알고리즘
다항회귀분석 : 두 변수간의 관계를 곡선 형태로 분석하는 알고리즘
'''
'''
단순 회귀 분석 : Y = aX+b
다항 회귀 분석 : Y = aX**2 + bX + c 비선형회귀분석
'''
# 다항식 변환 모듈 : PolynomialFeatures
from sklearn.preprocessing import PolynomialFeatures
# X : 독립변수, Y : 종속변수
# 다항식 변환
# degree = 2 : 2차항 의미
poly = PolynomialFeatures(degree=2)
# X_train : 훈련데이터
# X_train 데이터를 2차항 형식에 맞도록 변형
X_train_poly = poly.fit_transform(X_train)
print("원 데이터 :", X_train.shape)
print("2차항 변환 데이터:", X_train_poly.shape)
pr = LinearRegression() # 선형회귀분석 객체
pr.fit(X_train_poly, y_train) # 학습하기
# X_test : 검증데이터
X_test_poly = poly.fit_transform(X_test) # 2차항 형태로 변경
r_square = pr.score(X_test_poly, y_test) # 결정계수 (R-제곱)
print(r_square) #0.708...
y_hat_test = pr.predict(X_test_poly) # 2차항 형태로 변경된 테스트 데이터

# 산점도 그리기
fig = plt.figure(figsize=(10,5))
ax = fig.add_subplot(1,1,1)
# 원 데이터의 산점도 출력하기
ax.plot(X_train, y_train, 'o', label = 'Train Data')
# (X_test) 검증 데이터와 다항회귀분석의 결과값 (y_hat_test)
ax.plot(X_test, y_hat_test, 'r+', label = 'Predicted Value')
ax.legend(loc='best')
plt.xlabel('weight')
plt.ylabel('mpg')
plt.show()
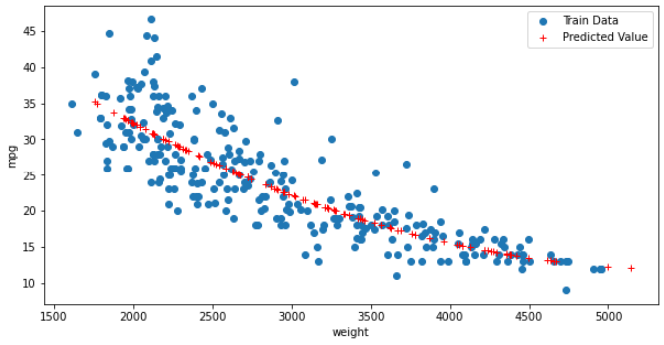
# 모형 전체 그래프 작성하기
X_poly = poly.fit_transform(X)
y_hat = pr.predict(X_poly)
plt.figure(figsize=(10,5))
ax1 = sns.kdeplot(Y, label='Y')
ax2 = sns.kdeplot(y_hat, label='y_hat', ax=ax1)
plt.legend()
plt.show()
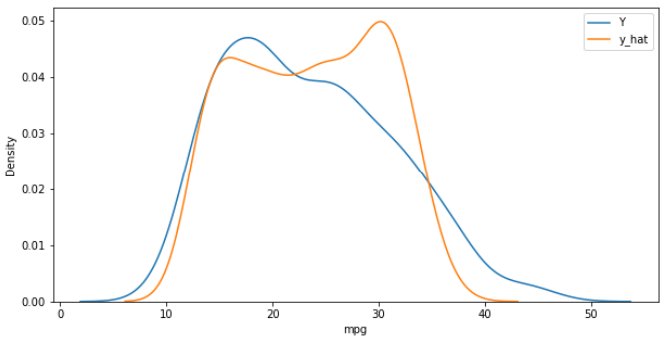
'''
단순회귀분석 : 독립변수, 종속변수가 한개
다중회귀분석 : 여러개의 독립변수가 종속변수에 영향을 주고, 선형관계를
갖는 경우
Y = b + a1*X1 + a2*X2 + ... + an*Xn
'''
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
X = ndf[['cylinders','horsepower','weight']]
Y = ndf['mpg']
# train data와 test data로 구분 (7:3 비율)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.3, random_state=10)
print('train data 개수:',X_train.shape)
print('test data 개수:',X_test.shape)
# X_train 훈련시키기
lr.fit(X_train, y_train)
r_square = lr.score(X_test, y_test)
r_square
# 회귀식의 기울기와 y절편 구하기
# 기울기
print("기울기 a", lr.coef_)
# y 절편
print("y 절편 b", lr.intercept_)
# test데이터로 예측하기
y_hat = lr.predict(X_test)
y_hat
# 예측된 데이터와 실데이터를 kdeplot으로 출력하기
plt.figure(figsize=(10,5))
ax1 = sns.kdeplot(y_test, label="y_test") #실제 mpg 데이터 그래프
ax2 = sns.kdeplot(y_hat, label='y_hat',ax=ax1)
plt.legend()
plt.show()

# 원 데이터로 예측하기
y_hat = lr.predict(X_test)
# 예측된 데이터와 실데이터를 kdeplot으로 출력하기
plt.figure(figsize=(10,5))
ax1 = sns.kdeplot(Y, label="Y") #실제 mpg 데이터 그래프
ax2 = sns.kdeplot(y_hat, label='y_hat',ax=ax1)
plt.legend()
plt.show()

'Python' 카테고리의 다른 글
| Python - SVM(서포트 벡터 머신) (0) | 2021.07.16 |
|---|---|
| Python - KNN(K-Nearest-Neighbors) (0) | 2021.07.16 |
| Python - 서울시 CCTV수를 파악해서 시각화하기 (산점도, 회귀선) (0) | 2021.07.14 |
| Python - 웹크롤링 후 텍스트 마이닝 (seleium) (0) | 2021.07.13 |
| Python - 웹크롤링 (BeautifulSoup/ Selenium) (0) | 2021.07.06 |



