<서론>
수학에서 쓰이는 수열과 집합의 연산은 코드에서는 반복문(loop, iteration)등으로 사용된다.
데이터 분석을 위해서는 많은 숫자의 합이나 곱을 계산해야 하기 때문에, 이러한 수학적 개념을 이해하는 것은 필수적이다. 우선 수열과 집합의 개념을 수식으로 이해해야 한다.
<수열>
수열은 N개의 숫자 또는 변수가 순서대로 나열된 것이다.
1, 2, 3, 4
𝑥₁ , 𝑥₂ , 𝑥₃ , 𝑥₄ , 𝑥₅ , 𝑥₆
<집합>
집합은 순서가 중요하지 않은 숫자들의 모임이다.
{1, 2, 3, 4}
{𝑥₁ , 𝑥₂ , 𝑥₃ , 𝑥₄ , 𝑥₅ , 𝑥₆}
<수열의 합과 곱>
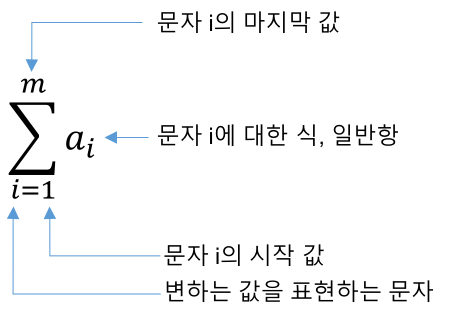
그리스 문자 Σ(시그마)와 Π(파이)의 기호를 이용하여, 간단하게 표시한다.
읽을 때는 각각 썸(합)과 프로덕트(곱)라고 읽을 수 있다.
합과 곱 아래에는 인덱스의 시작 값, 위에는 인덱스의 끝 값을 표시한다.

<중첩 반복>
만약, 중첩 반복의 경우 아래와 같은 수식으로 표현된다. (nested loop)
$$\sum_{i=1}^2[\sum_{i=1}^3(i+j)]$$ $$= \sum_{i=1}^2((i+1)+(i+2)+(i+3))$$ $$= ((1+1)+(1+2)+(1+3))+((2+1)+(2+2)+(2+3))$$
위와 같은 수식을 주피터 노트북이나 html 환경에서 표현하기 위해서는 아래와 같은 코드가 필요하다.
$$\sum_{i=1}^2[\sum_{i=1}^3(i+j)]$$
$$= \sum_{i=1}^2((i+1)+(i+2)+(i+3))$$
$$= ((1+1)+(1+2)+(1+3))+((2+1)+(2+2)+(2+3))$$
또한, 위의 반복 수열의 합을 아래 처럼 파이썬 for 문으로 표현할 수 있다.
sum = 0
for i in range(1,3):
for j in range(1,4):
sum = sum + (i + j)
'데이터를 위한 수학' 카테고리의 다른 글
| [4] 행렬의 표기법과 특수한 벡터와 행렬 (0) | 2022.02.13 |
|---|---|
| [3] 선형대수의 데이터 유형 (0) | 2022.02.07 |
| [1] 수학를 위한 그리스 문자 (0) | 2022.02.05 |
| [0] 수의 체계와 선형대수학 (0) | 2021.05.02 |



