기술 통계학
수집한 자료들을 정리하고 요약하여 자료가 어떤 특성을 갖고 있는지 해석하는 통계학의 한 분야
자료 요약 방법
1. 시각적인 방법(그래프)를 통한 자료 요약
2. 각종 통계 숫자를 이용한 자료의 요약
대표값 : 최빈값, 평균, 중앙값
-예시 데이터-
1. 최빈값 (Mode)
(1) 줄기-잎 그림으로 확인한 최빈값
data <- read.csv("cafedata.csv")
a <- data$Coffees
stem(a)

0 | 34444 0~4잔 : 3잔,4잔,4잔,4잔
0 | 5688 5~9잔 : 5잔,6잔,8잔,8잔
1 | 01134 10~14잔 : 10잔,11잔,11잔,13잔,14잔
1 | 668 15~19잔
2 | 001123344 20~24잔
2 | 55677789 25~29잔
3 | 001112334 30~34잔
3 | 55 35~39잔
4 | 1 40~44잔
4 | 8 45~49잔
(2) 최빈값 출력하기
table(a)
names(table(a))[which.max(table(a))]

2. 평균 (Mean)
- 평균은 변수의 값들의 합을 변수의 개수로 나눈 값이다.
- 이상값에 의해 값의 변동이 심하게 변할 수 있다.
mean(data$Coffees)
21.51064
-> 혹시 하나의 값이 480이 되어버리면 평균이 크게 달라진다. 이것은 평균의 약점이다.
3. 중앙값(= 중위수, Median)
- 모든 데이터 값을 크기 순서로 오름차순 정렬하였을 때, 중앙에 위치한 데이터 값으로 중앙값(중위수)라고 한다.
- 예를 들어 1, 2, 100의 세 값이 있을 때, 2가 가장 중앙에 있기 때문에 2가 중앙값이다. 값이 짝수개일 때에는 중앙값이 유일하지 않고 두 개가 될 수도 있다. 이 경우 그 두 값의 평균을 취한다. 예를 들어 1, 10, 90, 200 네 수의 중앙값은 10과 90의 평균인 50이 된다.
[R] median(data$Coffees)
23
-> 양 끝 값의 변화에 둔감하다. 이것은 중앙값의 장점이다.
분산
- 데이터가 평균으로부터 흩어진 정도
- 편차(데이터 -평균)의 합은 0이므로 편차의 제곱의 합을 이용하여 계산
- 모분산은 편차의 제곱의 합을 모집단의 수(N)으로 나누어주고, 표본분산은 표분의 수에서 1을 뺀 자유도(n-1)로 나누어 어 계산
* 자유도 (df = degree of freedom)
주어진 조건하에서 통계적 제한을 받지 않고, 자유롭게 변화될 수 있는 요소의 수
예를 들어, 평균이 4이고 아래의 총 변수의 갯수가 3개일 때,
각각 상황1,2,3처럼 2개의 변수가 주어졌을 때, 나머지 숫자는 5, 4, 3일 수 밖에 없다.
따라서, 샘플이 3개일 때, (자유롭게 지정할 수 있는) 요소의 수는 2개가 된다. 즉 n-1개가 자유도가 된다.
| 상황1 | 3 | 4 | ? |
| 상황2 | 4 | 4 | ? |
| 상황3 | 5 | 4 | ? |

표준편차
- 표준편차는 분산의 양(+)의 제곱근의 값이다.
- 분산은 편차의 제곱을 했기 때문에, 원래의 수학적 단위와 차이가 발생하므로, 제곱근을 취한 갓을 표준편차로 하고, 이 값을 통하여 평균에서 흩어진 정도를 나타낸다.

변동계수(CV; Coefficient of Variation)
- 상대 표준편차라고도 한다.
- 측정 단위가 서로 다른 자료의 흩어진 정도를 상대적으로 비교할 때 사용한다.
- 표준 편차나 분산은 한 가지 자료의 산포도를 측정하는 데는 유용하지만,단위가 다른 두 자료 군의 산포도를 비교하는 데는 부적절한다.
- 표준편차를 표본평균으로 나눈 값으로서 값이 클수록 상대적인 차이가 크다.
- 평균과 표준편차를 나누어서 단위가 없으므로 서로 다른 단위의 산포도를 비교할 수 있다.

| 구분 | 이쑤시개 | 지팡이 |
| 평균 | 10cm | 100cm |
| 표준편차 | 2cm | 2cm |
이쑤시개 공장과 지팡이 공장에서의 생산한 제품들의 표준편차는 위처럼 2cm로 동일하다.
하지만, 이쑤시개라는 제품의 2cm 차이와 지팡이라는 제품에서의 2cm 차이는 실제로 큰 차이를 가진다.
절대적 수치로 확인하면 비교가 어렵고, 상대적 수치로 표현한다.
| 구분 | 이쑤시개 | 지팡이 |
| 변동계수 | 2/10 = 0.2 | 2/100 = 0.02 |
즉, 이쑤시개가 지팡이보다 상대적 변동폭이 10배 더 크다.
-> 변동계수는 자료의 상대적인 변동폭을 비교하는 측도
4분위수
- 사분위수 범위는 자료들의 중간 50%에 포함되는 자료의 산포도를 나타낸다.
- 사분위 수 범위는 제 1사분위수(Q1)과 제 3사분위수(Q3) 사이의 차이이다.
| 순서 | 방법 | 예시 |
| 1 | 자료들을 오름 차순으로 정렬 | 1, 5, 8, 9, 13, 17 ,19 |
| 2 | 자료들의 중위수를 구함 | 7개의 자료로 홀수이므로, (7+1)/2 = 4번째 자료인 9가 중위수 |
| 3 | 중위수를 기준으로 좌측의 중위수(Q1)와 우측의 중위수(Q3)를 각각 구함 | 중위수를 기준으로 좌측(1 5 8)의 중위수 5 = Q1 / 우측 (13 17 19)의 중위수 17 = Q3을 구함 |
| 4 | 사분위 수 범위(IQR) = Q3 - Q1에 대입하여 IQR을 구함 | IQR = 17 -5 = 12 |
왜도
| 종류 | 설명 |
| 오른쪽 편포 | 최빈값 < 중위수 < 평균 오른쪽꼬리 분포 왜도 > 0 |
| 왼쪽 편포 | 평균 < 중위수 < 최빈값 왼쪽꼬리 분포 왜도 < 0 |
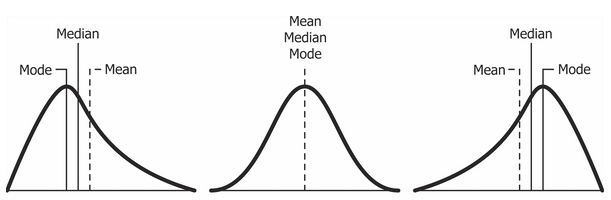
a. 오른쪽 편포 (왜도>0)
예시, 2 3 3 4 5 6 7 8 9 10 11 12 13
최빈값 3 < 중위수 7 < 평균 7.1
b. 정규분포
예시, 2 3 4 5 5 5 5 5 5 5 6 7 8
최빈값 5 = 중위수 5 = 평균 5
c. 왼쪽 편포 (왜도<0)
예시, 2 3 4 5 6 7 8 9 10 11 12 12 13
평균 7.8 < 중위수 8 < 최빈값 12
첨도
- 데이터의 분포가 정규 분포 곡선으로부터 위 또는 아래쪽으로 뾰족한 정도를 보여주는 값이다.
- 정규 분표는 첨도가 3이지만, 일반적으로 첨도의 정의에서 3을 뺀 0을 기준으로 하고 있다. 따라서 이 책에서도 정규 본포의 첨도를 0으로 한다.

'통계학' 카테고리의 다른 글
| t-test (0) | 2021.12.19 |
|---|---|
| 표준정규분포 (0) | 2021.12.11 |
| 회귀분석(Regression) (0) | 2021.12.05 |
| 상관관계(공분산, 상관계수) (1) | 2021.11.18 |
| t-test (0) | 2021.07.12 |



