1. 상관관계란?

기온을 x로 판매량을 y로 순서쌍으로 표시
ex) (14.2, 215)
좌측의 표를 이용하여, 우측의 산점도로 그린다.
즉, 순서쌍을 그래프 위 점으로 표현한다.
이럴 경우, 점들이 일정한 패턴을 나타낼 수 있는데,
위의 예시에서는, 기온이 오를수록 아이스크림의 판매량도 오른다고 볼 수 있다.
반대로, 기온이 떨어질수록 아이스크림의 판매량은 떨어진다.
즉, 두가지의 변량 사이의 일정한 관계가 성립한다고 볼 수 있다.
=> 상관관계 : 두 가지의 변량 사이의 관계
양의 상관관계 : x값이 커지면 y의 값도 커진다.
음의 상관과계 : x값이 작아지면 y의 값도 작아진다.


기울기 > 0,
y의 증가량 / x의 증가량

2. 공분산이란?
X나 Y의 분산은 X나 Y의 값이 얼마나 퍼져있는지를 표현한 것이다.
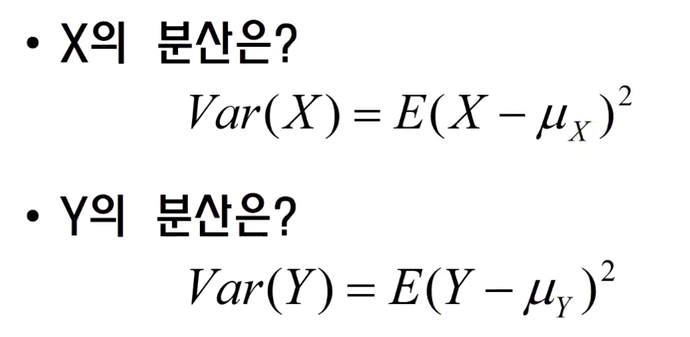
X, Y의 공분산은 X와 Y가 어떠한 방향성을 가지고 있는지를 표현한 것이다.
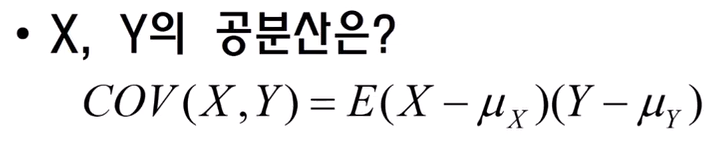
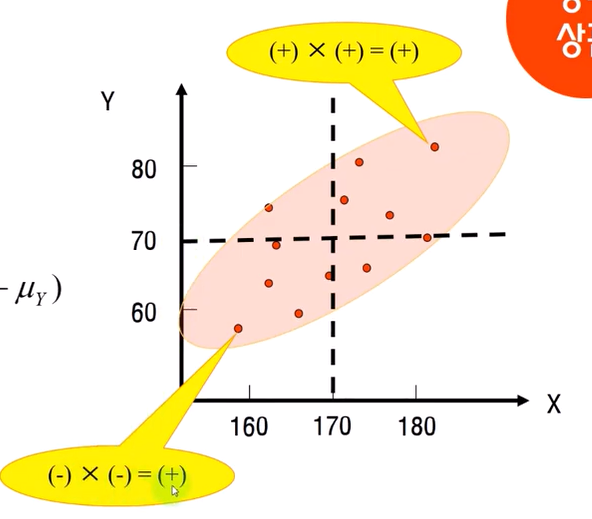
공분산에 대한 설명을 하자면,
아래의 표에서 X의 평균은 170 Y의 평균은 70이다.
그때 (X - m)(Y - m) = (+) x (+) = + 가
또는, (X - m)(Y - m) = (-) x (-) = + 가 된다.
이럴 때, 양의 상관이라고 한다.
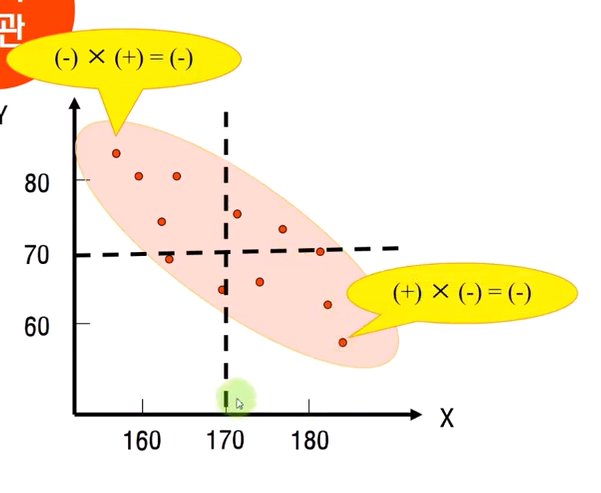
음의 상관인 경우에는,
그때 (X - m)(Y - m) = (-) x (+) = - 가
또는, (X - m)(Y - m) = (+) x (-) = - 가 된다.
따라서,
양의 상관일때는 E(X - m)(Y - m)의 값이 커지고,
음의 상관일때는 E(X - m)(Y - m)의 값이 작아지고,
무상관이면 E(X - m)(Y - m)의 값이 0에 가까워진다.
* 공분산의 특징
1. 상관관계의 상승 혹은 하강하는 경향을 이해할 수 있다.
2. 공분산 값의 크기는 측정 단위에 따라 달라지므로, 선형관계의 강도를 나타내지는 못한다.
ㄴ 공분산을 표준화 해준 궁극적인 연관성의 척도는 상관계수(Correlation Coefficient)
3. 상관계수란?
모상관계수 :
X, Y의 공분산을 각각의 편차로 나누어준다.
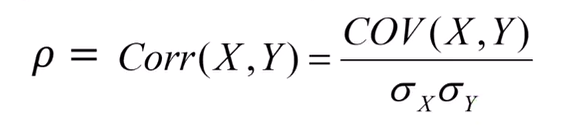
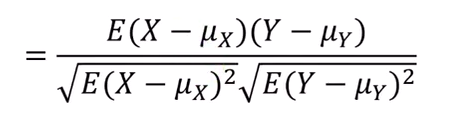
스피어만 상관계수 :
분석하고자하는 두 연속형 변수의 분포가 심각하게 정규분포를 벗어난다거나, 표본크기가 작을 때 또는 두 변수가 순위 척도 자료일 때 사용하는 방법이다. 데이터의 순서에 의미를 부여한 데이터 변수. ex) 성적 순위(1,2,3등), 학력(중졸, 고졸, 대졸) -> 데이터에 순위만 매길 수 있다면, 적용이 가능하기 때문에 연속형 데이터와 순서형 데이터에 적용할 수 있다.
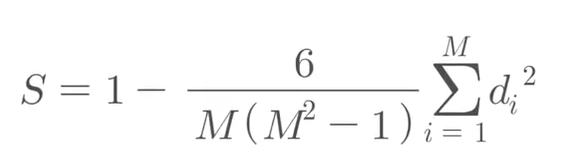
d¡는 두 변수의 값들을 크기 순으로 정렬한 것에서 i번째 값의 차를 의미한다. 한 변수 값이 커지면 다른 변수의 값도 단조롭게 커지는지 알아보기 위한 것이다. 스피어만 상관계수가 1에 가까울수록 좋은 단조 상관성을 갖고 있는 것이고, 0에 가깝다면 단조 상관성이 거의 없는 것이다.
피어슨 상관계수(표본 상관계수) :
모상관계수에서 x의 모평균 대신에 x의 표본 평균을 넣어주고,
y의 모평균 대신에 y의 표본 평균을 넣어준다. 위의 E(평균)은 토탈 합 나누기 갯수로 표현되는데, 아래 식에서는
위 아래의 분모가 지워진것.
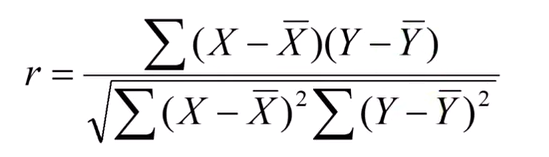
상관계수의 범위 : -1과 1 사이
상관계수가 1일 경우 : X와 X의 상관계수
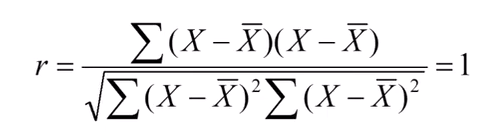
상관계수가 -1일 경우 : X와 -X의 상관계수
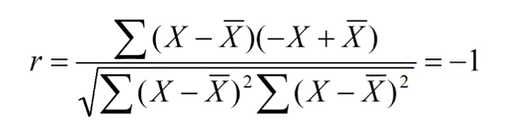
EX) 8명의 언어 점수와 수학 점수의 표본 상관 계수 구하기
| x | y | x - x bar | y - y bar | (x - x bar)(y - y bar) | (x - x bar )^2 | (y - y bar)^2 |
| 36 | 35 | -24 | -15 | 360 | 576 | 225 |
| 80 | 65 | 20 | 15 | 300 | 400 | 225 |
| 50 | 60 | -10 | 10 | -100 | 100 | 100 |
| 58 | 39 | -2 | -11 | 22 | 4 | 121 |
| 72 | 48 | 12 | -2 | -24 | 144 | 4 |
| 60 | 44 | 0 | -6 | 0 | 0 | 36 |
| 56 | 48 | -4 | -2 | 8 | 16 | 4 |
| 68 | 61 | 8 | 11 | 88 | 64 | 121 |
| ∑480 | ∑400 | 0 | 0 | 654 | 1304 | 836 |
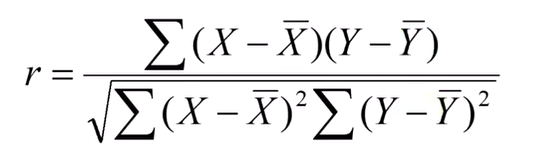
654 / (√1304*√836) = 0.63
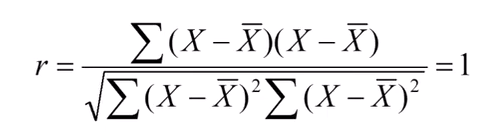
1304 / 1304 = 1
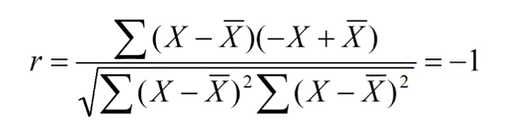
(-) 1304 / 1304 = -1
* 상관계수의 한계 :
1. 상관계수는 만능이 아니다.
2. 수학적 관계이지 속성의 관계는 아니다
ex) 언어를 잘하는 사람은 수학도 잘 할 가능성이 있지만,
수학을 잘하기 위해서 언어 공부를 열심히 해야 하는 것은 아니다. (인과 관계 X)
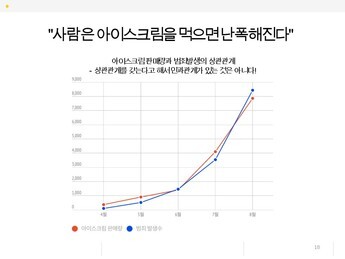
->유명한 사례, 아이스크림과 범죄율 간의 상관관계는 있지만, 인과 관계는 없다.
ㄴ 날씨가 더워서 나타난 상관 관계일 뿐...
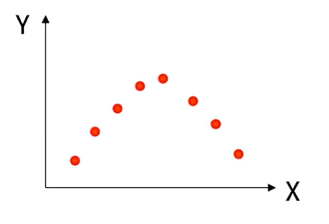
3. 선형관계의 측도이다.
그래프가 선형성을 가지지 않더라도, x와 y의 관계성이 있을 수 있다. 아래와 같은 곡선 관계는 찾아내지 못한다.
4. 따라서 자료 분석의 초기 단계에만 사용될 수 있다.



